- 论文:https://www.aclweb.org/anthology/2020.emnlp-main.18/
Abstract & Intro
将句法分析树嵌入到人工神经网络并可视化语法推理
用显式通用句法解释(句法分析树)改进最新的通用句子嵌入,并创建在句法上可解释的神经网络结构
循环神经网络[RecNNs]是应用于二叉树的递归神经网络。
结构核函数[structural kernel function]一直是学习中利用句法信息的方法,但这些函数不能在神经网络中使用。核机器[kernel machine]利用了这些通常是递归的结构核函数,它们定义了计算公共子结构的两棵树之间的相似性度量。
结构核领域,分布式内核为了降低树核的计算量,这些分布式树核将巨大的子结构空间嵌入到较小的空间中。这种嵌入是通过使用递归函数来获得的,递归函数相对于树的大小是线性的。[ Distributed tree kernels.]
Reverse Feature Engineering of Syntactic Tree Kernels[2010]
3. The model
- 介绍Kernel-inspired Encoder with a Recursive Mechanism for Interpretable Trees(KERMIT),及其可视化工具\(\bold {KERMIT}_{viz}\),可以与transformer网络结合使用。
3.1 预备表示(Preliminary notation)
- 修正了解析树、随机向量和对随机向量操作的表示。
- 解析树\(\mathcal{T}\)和解析子树\(\tau\)被递归定义为\(t=(r,[t_1,...,t_k])\),其中\(r\)是树根的表示,\([t_1,...,t_k]\)是子树\(t_i\)的集合。叶子节点\(t\)被定义为\(r=(r,[])\),其中的子树集合为空,也可直接记作\(t=r\)
- 对于解析树\(\mathcal{T}\),模型需要三个子树集合的定义:集合\(N(\mathcal{T})\)、集合\(\bar S(\mathcal{T})\)和集合\(S(\mathcal{T})\)。后两个集合根据我们想要在通用句法embedding中建模而用到的子树定义。
- \(N(\mathcal{T})\)包含\(\mathcal{T}\)的所有完整子树。给定一棵树\(\mathcal{T}\)和其中一个结点\(r\),\(\mathcal{T}\)的一个完整子树是以\(r\)为根一直到达叶子节点的子树。

- \(\bar S(\mathcal{T})\)
- \(N(\mathcal{T})\)包含\(\mathcal{T}\)的所有完整子树。给定一棵树\(\mathcal{T}\)和其中一个结点\(r\),\(\mathcal{T}\)的一个完整子树是以\(r\)为根一直到达叶子节点的子树。
- 最后,为了构建未经训练的KERMIT编码器,我们利用从多变量高斯分布\(v\sim \mathcal{N}(d,\frac 1 {\sqrt{d}})\)中提取出的随机向量的性质。这些向量保证了如果\(u ≠v\),则\(u^Tv≈0\)并且\(u^Tu≈1\)。这个性质对于可解释性很重要。
- 为了合成这些向量,我们利用混洗循环卷积(shuffled circular convolution)\(u\otimes v\)。如何这些向量取自多元高斯分布,则该函数保证\((u\otimes v)^Tu≈0,(u\otimes v)^Tv≈0,(u\otimes v)≠(v\otimes u)\)。这是一步循环卷积(circular convolution)的操作。这一步操作对于合理合成节点向量很重要。
3.2 解析树及其子网络的编码器(The encoder for parse trees and its
sub-network)

- 主要有两个组件。第一个是Kermit编码器,它将解析树\(\mathcal{T}\)实际编码为嵌入向量。 \[ y=\mathcal{D}(\mathcal{T}) \] 第二个组件是利用这些嵌入向量的多层感知器: \[ z=mlp(y) \]
第一个组件
编码器\(\mathcal{D}\)来源于树核(tree kernel)和分布式树核(distributed tree kernel)。它使得在向量空间\(R^d\)内表示解析树成为可能,这个空间承载了大量子树\(R^n\)的空间,其中\(n\)是不同子树的数目。
每个\(\mathcal{T}\)使用它的有效子树\(S(\mathcal{T})\)表示。
编码器是基于树节点标签\(x_r=W_or\in R^d\)的嵌入层和基于混洗循环卷积\(\otimes\)的递归编码函数。
嵌入层\(x_r=W_or\in R^d\)是未经训练的编码函数,其将一个树节点标签\(r\)的one-hot向量\(r\)映射到先前介绍的多变量高斯分布\(v\sim \mathcal{N}(d,\frac 1 {\sqrt{d}})\)中提取到的随机变量。
所以\(W_o\in R^{m×d}\)是一个\(m\)列的矩阵,其中\(m\)是节点标签集合的基数,并且矩阵\(W_o\)中每一列\(w^{(i)}\)都满足\(w^{(i)}\sim \mathcal{N}(d,\frac 1 {\sqrt{d}})\)。函数\(\mathcal{D}(\mathcal{T})\)被定义为解析树上的递归函数\(\Upsilon(t)\)的和: \[ y=\mathcal{D}(\mathcal{T})=\sum_{t\in N(\mathcal{T})}\Upsilon(t) \] 其中,\(N(\mathcal{T})\)之前定义为是完整子树\(\mathcal{T}\)的集合,然后\(\Upsilon(t)\)被定义为:
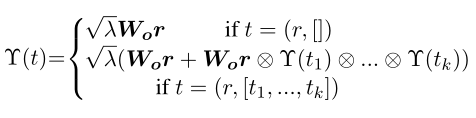
其中,\(0<\lambda≤1\)是惩戒大子树的衰减因子。通过动态算法实现\(\mathcal{D}(\mathcal{T})\)计算成本是相对于树的节点是线性的,并且基本函数的\(\otimes\)的花销是\(dlogd\),\(d\)是表示空间\(R^d\)的大小。
由于其本质,树神经编码器有一个很好地解释为一个非常简单的嵌入层即\(W_{\Upsilon}\in R^{d×n}\),将子树的空间嵌入到较小的\(R^d\)空间中,因此\(\mathcal{D(T)}\)可看作: \[ y=\mathcal{D(T)}=W_{\Upsilon}x \] 其中\(x\)为子树集合\(S(\mathcal{T})\)的向量表示,即\(\sqrt{\lambda^k}x_t\)的和,其中\(x_t\)是表示\(t\in S(\mathcal{T})\)的one-hot向量,\(\lambda\)是惩戒规模大的树的衰减因子,\(k\)是树\(t\)的节点数目。可以很容易的推导出,矩阵\(W_\Upsilon\)中列\(w_i\)编码子树\(t\)如下:
