Graph Convolution over Pruned Dependency Trees Improves Relation Extraction

Abstract & Intro

提出了一种基于图卷积网络的关系提取神经模型，使得它能够有效地并行汇集任意依赖结构上的信息
对输入树应用了一种新的剪枝策略，即两个实体之间可能存在关系的最短路径附近保持单词。帮助基于依赖的模型在不破坏关键内容的情况下最大限度地去除无关信息，以提高其鲁棒性
证明了基于依赖的模型与序列模型具有互补的优点。
通过图卷积运算对输入句子上的依存结构进行编码，然后提取以实体为中心的表示以做出稳健的关系预测。还应用了一种新的以路径为中心的剪枝技术，在最大限度地保留相关内容的同时从树中删除不相关的信息。

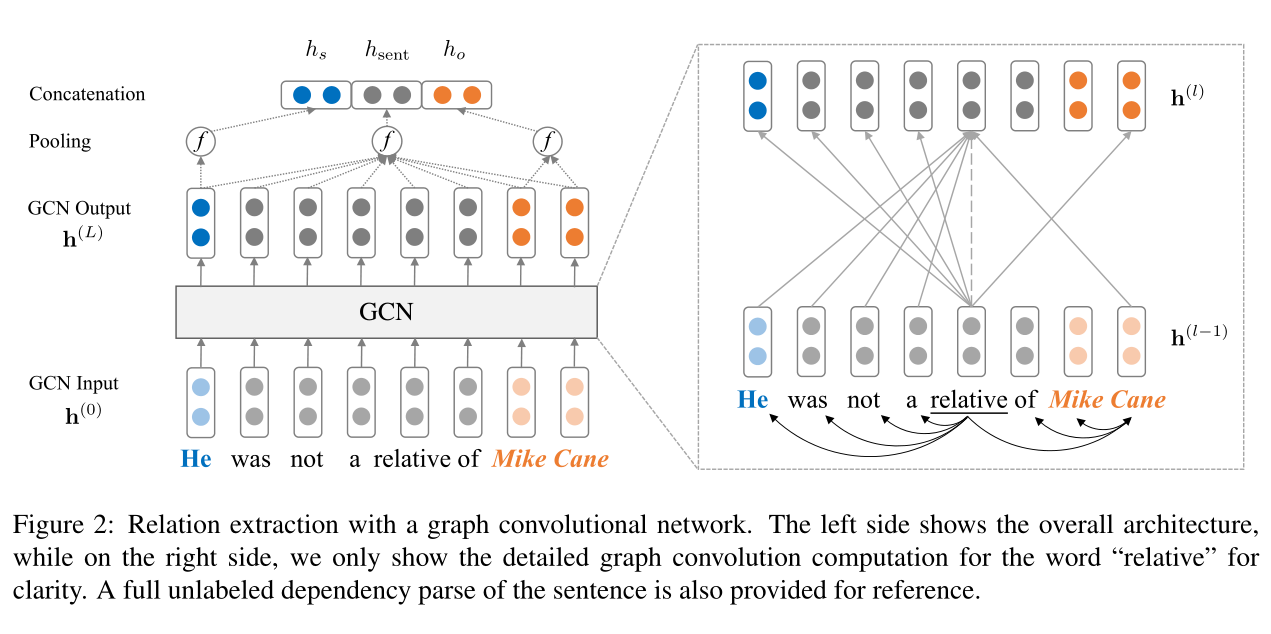
将每棵树转换为其对应的邻接矩阵\(A\)(图表示)使得图卷积操作适合于建模依赖树，其中如果标记\(i\)和\(j\)之间如果存在依赖边，则\(A_{ij}=1\)。
因为token的度数变化很大，直接应用图卷积神经网络的公式会导致句子表示偏向于度数高的结点而不考虑节点中携带的信息(详见Sec. 2.2)，同时\(h_i^{(l-1)}\)中的信息永远不会传递到\(h_i^{(l)}\)，因为节点在依赖树中不会连接到自己。
故在\(L\)层GCN中，假设共有\(n\)个节点，\(h_i^{(l-1)}\)表示为第\(l\)层的输入向量，\(h_i^{(l)}\)表示为第\(l\)层的输出向量，公式更改为： \[ h_i^{(l)}=\sigma(\sum_{j=1}^n\tilde A_{ij}W^{(l)}h_j^{(l-1)}/d_i+b^{(l)}) \] 其中\(\tilde A=A+I\)，\(I\)为\(n×n\)的单位矩阵，\(d_i=\sum_{j=1}^n\tilde A_{ij}\)是在结果图中token i的度数，\(W^{(l)}\)是线性变换，\(b^{(l)}\)是偏置项，\(\sigma\)是非线性函数（例如，ReLU）
好处：可通过矩阵乘法高效实现，这使得它非常适合在示例上进行批处理计算和在GPU上运行。此外，令牌之间的信息传播是并行进行的，运行时不依赖于依赖树的深度。
上述GCN模型对依赖图中所有边使用相同的参数。

设\(\chi=[x_1,...,x_n]\)表示一个句子，\(x_i\)是第\(i\)个令牌(token)。主语实体和宾语实体被标识出并分别对应句子中的两个跨度(span)：\(\chi_s=[x_{s_1},...,x_{s_2}]\ \ \chi_o=[x_{o_1},...,x_{o_2}]\)，给定\(\chi,\chi_s,\chi_o\)，关系提取的目标是预测实体之间存在的关系\(r\in R\)（预定义的关系集），否则为“无关系”。
在对词向量应用\(L\)层GCN后，得到了每个令牌的隐藏表示，为了利用这些单词表示进行关系提取，首先获得如下句子表示法： \[ h_{sent}=f(h^{(L)})=f(GCN(h^{(0)})) \] \(h^{(l)}\)表示第\(l\)层GCN的集体隐藏表示，\(f:R^{d×n}\rightarrow R^d\)是从\(n\)个输出向量映射到句子向量的max-pooling。
依赖树中接近实体token的信息通常是关系分类的中心。因此我们也从\(h^{(L)}\)中获得了主语表示： \[ h_s=f(h^{(L)}_{s_1:s_2}) \] 同样的方法也可以得到\(h_o\)的表示
将句子和实体表示连接起来，并将它们馈送到前馈神经网络(FFNN)中来获得用于分类的最终表示： \[ h_{final}=FFNN([h_{sent};h_s;h_o]) \] 然后\(h_{final}\)被馈送到线性层随后进行\(SoftMax\)运算以获得关系上的概率分布。

与关系相关的大部分信息通常包含在以两个实体的最短公共祖先(LCA)为根的子树中。将GCN模型与树修剪策略相结合以进一步提高性能。但是过于激进的修剪(例如只保留依赖路径)可能会导致关键信息丢失，反过来影响健壮性。例如：
提出了以路径为中心的剪枝(path-centric pruning)。在LCA子树里添加距离依赖路径最远\(K\)个路径的令牌来实现的。\(K=0\)，相当于将树向下修剪到路径，\(K=1\)保留直接连接到路径的所有节点，\(K=∞\)保留整个LCA子树。
将剪枝后的树直接反馈到GCN中(LSTM仍然作用于整个句子)，发现\(K=1\)的剪枝在包含相关信息(例如否定和合取)和尽可能地将不相关的内容排除在所得到的剪枝树之间达到了最佳的平衡。