- 论文地址:https://ink.library.smu.edu.sg/cgi/viewcontent.cgi?article=5939&context=sis_research
1. Introduction
迭代的增长候选关系路径,最终到候选答案。每次迭代修剪掉不太可能到正确答案的分支。
采用match-aggregate框架将问题与候选答案序列进行匹配。提出一种增量式序列匹配模型来计算匹配分数,而不需要重新访问关系路径中的早期关系。
无需假设跳数已知等
由3个模块组成:迭代路径增长、增量序列匹配和终止检查。【3跳数据集】
3. Our Method
3.1 迭代路径增长(Iterative Path Growth)
- 迭代路径增长将候选路径增长到\(T\)跳,每次迭代一跳。在每次迭代结束时,它只保留与问题最匹配的前K个候选路径。
3.1.1 Candidate path
- 给定问题\(q\),首先确定主题实体(topic entity)\(e_0\),候选路径是起始于\(e_0\)的实体和关系的序列,使用\(p=(e_0,r_1,e_1,r_2,e_2,...,r_t,e_t)\)表示\(t\)跳的候选路径。
3.1.2 Candidate path set
- 在第\(t\)次迭代后的候选路径集合定义为在第\(t\)次迭代结束时保留的前\(K\)条候选路径的集合,用\(\mathcal{P}^{(t)}\)表示。\(|\mathcal{P}|=K\),\(each\ p\in \mathcal{P}^{(t)}\)有\(t\)跳关系。
3.1.3 Tail entity
- 候选路径\(p\)的最后一个实体。
3.1.4 总结算法

3.2 增量序列匹配(Incremental Sequence Matching)
因为路径是迭代增长,在第\(t\)此迭代中,当需要匹配候选路径\(p\in \tilde{\mathcal{P}}\)时,前\(t-1\)个关系时的\(p\)已经与先前迭代中的问题匹配完了,故只需将最后一个关系\(p\)与问题进行匹配,并将此迭代中的分数与前几次迭代分数聚合起来,故为增量。
问题表示为:\(Q=(q_1,q_2,...,q_m)\),其中\(q_i\)是问题中第i个词的embedding向量。
对于候选路径\(p=(e_0,r_1,e_1,...,r_t,e_t)\),表示为\(P^{(t)}=(w_{r_t,1},w_{r_t,2},...,w_{r_t,n})\),其中\(w_{r_t,j}\)是关系\(r_t\)的第\(j\)个词的embedding向量。只考虑\(r_t\)而不考虑其他关系,因为我们是增量的。也无需考虑各个实体。
然后考虑两组注意力权重:一组在Q(\(\beta\))上归一化,一组在\(P^{t}\)(\(\alpha\))上归一化。
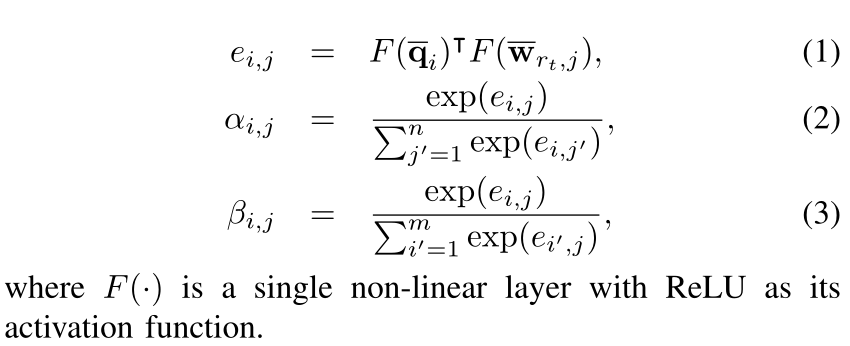
为衡量\(P^{(t)}\)与\(Q\)的匹配程度,对于\(Q\)中每个单词\(q_i\),推导出注意力加权和\(\bar P^{(t)}\)如下: \[ v_i^{(t)}=\sum_{j=1}^n\alpha_{i,j}\cdot \bar w_{r_t,j} \] 可以将\(\bar q_i\)与\(v_i^{(t)}\)进行比较,衡量问题中的第\(i\)个单词通过关系\(r_t\)在当前迭代中的匹配程度。
因为做的是增量匹配,可能\(\bar q_i\)已在\(p_{(t-1)}\)中与其他单词匹配过,故在当前阶段\(\bar q_i\)与\(r_t\)的匹配可能不关键。故定义标量\(a_i^{(t)}\)来记录路径\(p\)中到第\(t\)次迭代得匹配程度,首先设置\(a_i^{(0)}=0\),然后定义 \[ a^{(t)}_i=a^{(t-1)}_i+\sum_{j=1}^n\beta_{i,j} \] 与\(Q\)中其他单词相比,\(\sum_{j=1}^n\)直观展示了\(q_i\)与\(r_t\)中所有单词的匹配程度。
匹配向量(matching vector):

给定序列\((m_1^{(t)},m_2^{(t)},...,m_m^{t})\),使用LSTM来处理该序列,然后进行maxpooling来获得单个向量\(\bar m^{(t)}\): \[ \bar m^{(t)}=Max-Pool(LSTM(m_1^{(t)},m_2^{(t)},...,m_m^{t})) \]
然后使用该向量导出\(Q\)和\(P^{(t)}\)的匹配分数,如下图:
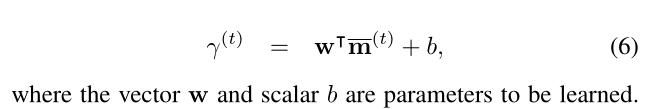
整个候选路径\(p\)和问题之间的完全匹配分数定义为如下,其中\(s^{(0)}(\cdot)=1\),对于有\(t\)个关系的\(p\)来说: \[ s^{(t)}(p)=s^{(t-1)}(p_{t-1})\cdot \gamma^{(t)} \] \(s^{(t)}(\cdot)\)之后被用来rank\(\tilde{\mathcal{P}}\),来获得\(\mathcal{P}^{(t)}\)。
3.3 终止检查(Termination Check)
向量\(\bar m^{(t)}\)是对\(p\)相对于\(q\)的匹配程度进行编码,将其转换为单个值便于终止检查,首先在第\(t\)次迭代中为每个候选路径\(p\)定义以下分数

在预测阶段,将\(\bar z(T)\)与阀值\(\tau\)进行比较以确定何时停止。
3.4 损失函数
需要学习的参数:

希望终止时\(\bar z^{(t)}\)接近1,反之接近0
对于\(each\ p\in \mathcal{P}^{(t)}\),通过比较tail entity(或者tail entities)与正确答案entity或entities,可以计算F1分数,然后使用以下公式进行归一化:

第二个目标是终止检查:
