1. Introduction
只能以最终答案为参考,而在中间步骤缺乏监督信号,学生网络的目标是找到问题的正确答案,教师网络则是试图学习中间监督信号以提高学生网络的推理能力,具体地说,教师模型推断中间步骤的哪些实体与问题更相关,并且这些实体被认为是中间监督信号。主要创新点是教师网络的设计,利用向前向后推理来增强中间实体分布的学习,教师网络可以产生更可靠的中间监督信号,解决虚假推理。
监督信号一般为<question, answer>而不是<question, relation path>。
双向搜索算法,向前和向后搜索来更有效地识别。我们也有两种不同的观点来考虑任务设置:寻找从主题实体(即查询中的实体)到答案实体的路径的正向推理和从答案实体返回到主题实体的反向推理。
学生网络采用神经状态机(NSM)来实现,学生网络可以根据从教师网络学习到的中间实体分布来改进自己。
4. 提出的方法
4.1 Overview
- 学生网络基于NSM,通过将知识库看作一个图,使其适应于多跳KBQA任务,并在多跳推理过程中保持逐步学习的实体在实体上的分布。教师网络是对NSM的体系结构进行了改进,加入了一种新颖的双向推理机制,使其能够在中间推理步骤中学习到更可靠的实体分布,这些实体分布随后将被学生网络用作监督信号。
4.2 Neural State Machine for Multi-hop KBQA
- 由指令部件和推理组件组成,指令组件向推理组件发送指令向量,而推理组件判断实体分布并学习实体表示。
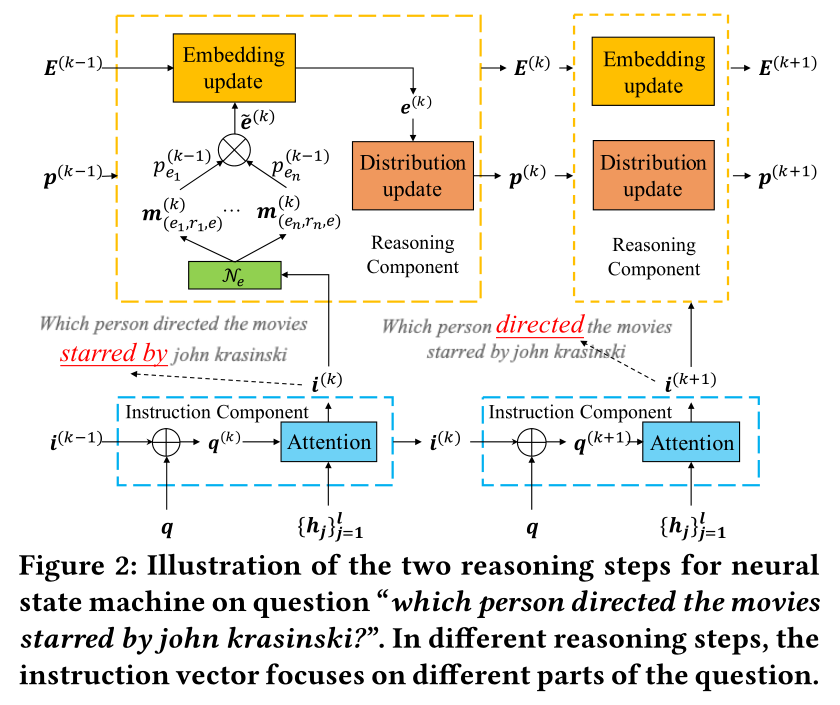
4.2.1 指令组件(Instruction Component)
先描述将给定的自然语言问题转换为一系列控制推理过程的指令向量。
指令组件的输入由查询嵌入和来自前一个推理步骤的指令向量组成。
初始向量为0向量。利用GloVe获得查询词的嵌入,然后利用LSTM网络获得一组隐藏层\(\{h_j\}^l_{j=1}\),其中\(h_j\in R^d,l\)是查询的长度,最后一个隐藏层状态为问题表示即\(q=h_l\)。令\(i^{(k)}\in R^d\)为第\(k\)步推理的指令向量,采用下列方法学习指令向量\(i^{(k)}\): \[ i^{(k)}=\sum_{j=1}^l\alpha_j^{(k)}h_j,\\ \alpha_j^{(k)}=softmax_j(W_\alpha(q^{(k)}\odot h_j)+b_{\alpha}),\\ q^{(k)}=W^{(k)}[i^{(k-1)}:q]+b^{(k)}. \]
其中\(W^{(k)}\in R^{d×2d},W_{\alpha}\in R^{d×d},b^{k}、b_{\alpha}\in R^d\)都是需要学习的参数。
核心思想是学习不同时间步的指令向量时关注查询的特定部分。同时动态更新查询表示,以便包含先前指令向量的信息,通过重复以上步骤,可以在\(n\)步推理后获得指令向量列表\(\{i^{(k)}\}^n_{k=1}\)。
4.2.2 推理组件(Reasoning Component)
获得指令组件\(i^{k}\)后,我们可以将其用作推理信号的指导信号。
推理组件的输入包括当前步骤的指令向量、以及上一步推理步骤中获得的实体分布(entity distribution)和实体嵌入(entity embeddings)。首先,考虑涉及\(e\)的关系来设置初始实体嵌入: \[ e^{(0)}=\sigma(\sum_{(<e',r,e>\in N_e)}r\cdot W_T) \] 其中\(W_T\in R^{d×d}\)是需要学习的参数,没有用到\(e\)的嵌入来初始化,因为重要的是关系不是实体。
给定三元组\(<e',r,e>\),匹配向量\(m_{<e',r,e>}^{(k)}\)通过匹配当前指令向量\(i^{(k)}\)与关系向量\(r\)来获得: \[ m_{<e',r,e>}=\sigma(i^{(k)}\odot W_Rr) \] \(W_R\in R^{d×d}\)是需要学习的参数。
最后我们聚合来自相邻三元组的匹配信息,并根据它们在上一推理步骤中受到的关注程度来为其分配权重。 \[ \tilde e^{(k)}=\sum_{<e',r,e>\in N_e}p^{(k-1)}_{e'}\cdot m^{(k)}_{<e',r,e>'} \] 其中\(p_{e'}^{(k-1)}\)是上一推理步骤中实体\(e'\)的分配概率。这样的表示能捕获与知识库中实体相关联的关系语义。
然后更新实体嵌入如下: \[ e^{(k)}=FFN([e^{(k-1)};\tilde e^{(k)}]) \] 其中,FFN是以上一步嵌入\(e^{(k-1)}\)及关系聚合embedding\(\tilde e^{(k)}\)为输入的前反馈层。
通过此过程,关系路径(从topic entities到answer entities)和它与问题的匹配程度都编码到节点嵌入中去。在步骤\(k\)导出的中间实体上的概率分布可计算为: \[ p^{(k)}=softmax(E^{ {(k)}^T}w) \] 其中\(E^{(k)}\)是一个矩阵,每一列为第\(k\)步的实体嵌入,\(w\)为参数。
4.3 The Teacher Network
- 目标是在中间步骤中学习或推断可靠的实体分布。没有这样的标签实体分布来训练教师网络,故受双向搜索算法启发,结合了双向推理机制来增强教师网络中中间实体分布的学习。
4.3.1 多跳KBQA的双向推理
考虑forward reasoning和backward reasoning,让这两个推理过程在中间步骤相互同步。这样派生的中间实体分布比从单一方向学习的分布更可靠。
给定\(n\)跳推理路径,让\(p_f^{(k)}\)和\(p_b^{(n-k)}\)分别表示前向推理第\(k\)步和后向推理第\(n-k\)步的实体分布。正常情况下\(p_f^{(k)}≈p_b^{(n-k)}\)。
4.3.2 推理体系结构(Reasoning Architectures)
有两种神经结构:并行推理和混合推理
并行推理(parallel reasoning):建立两个独立地NSM分别用于正向和反向推理,这两个网络相互独立,不共享参数,只考虑在中间实体分布上加上对应约束。
混合推理(hybrid reasoning):共享相同的指令组件,并将两个推理过程安排在一个循环流水线中。除了对应约束之外,这两个进程还接收相同的指令向量。此外,在正向推理的最后一步中导出的信息作为初始值被馈送到反向推理中。在形式上,以下公式在这种情况下成立: \[ p_b^{(0)}=p_f^{(n)},E_b^{(0)}=E_f^{(n)},\\ i_b^{(k)}=i_f^{(n+1-k)} \]
两种结构图如下:

并行推理具有更松散的集成,而混合推理则需要两个推理过程中的信息进行更深层次的融合。与双向BFS不同,在我们的任务中,反向推理可能无法准确模拟正向推理的反向过程,因为这两个过程对应于多跳KBQA中不同的语义。考虑到这一问题,我们共享指令向量,并循环正向推理的最终状态来初始化后向推理。通过这种方式,反向推理获得了更多关于正向推理的信息,从而可以更好地追溯正向推理的推理路径。
4.4 通过学生-教师框架学习
4.4.1 Optimizing the Teacher Network
教师网络主要考虑两个方面的损失,即推理损失和通信损失。
推理损失反映了对准确实体的预测能力,分成两个方向 \[ \mathcal{L}_f=D_{KL}(p_f^{(n)},p^{*}_f),\ \mathcal{L}_b=D_{KL}(p_b^{(n)},p_b^{*}) \] 其中\(p_f^{(n)}\)(\[p_b^{(n)}\])表示前向(后向)推理过程中最后的实体分布。\(p_f^*\)及\(p_b^*\)表示真实的实体分布。\(D_{KL}(\cdot,\cdot)\)表示Kullback-Leibler发散,以不对称的方式测量两个分布之间的差异。
为了获得\(p_f^*\)和\(p_b^*\)我们将正确实体出现的次数转化为频率归一化分布。例如,如果图中\(k\)个实体是正确实体,则最终分布中为他们分配\(\frac{1}{k}\)的概率。
通信损失反映了两个推理过程的中间实体分布之间的一致性。可以通过计算每个中间步骤的损失相加来计算: \[ \mathcal{L}_c=\sum_{k=1}^{n-1}D_{JS}(p_f^{(k)},p_b^{(n-k)}) \] 其中\(D_{JS}(\cdot,\cdot)\)是Jensen-Shannon散度,以对称的方式测量两个分布之间的差异。
最后教师网络整体的损失函数\(\mathcal{L}_t\)为: \[ \mathcal{L}_t=\mathcal{L}_f+\lambda_b\mathcal{L}_b+\lambda_c\mathcal{L}_c \]
其中\(\lambda_b\ and\ \lambda_c\in(0,1)\)是控制因子权重的超参数。
4.4.2 Optimizing the Student Network
对教师模型进行收敛训练后,可以得到教师网络两个推理过程中的中间实体分布。我们将两个分布的平均值最为监督信号: \[ p_t^{(k)}=\frac{1}{2}(p_f^{k}+p_b^{(n-k)}),\ k=1,...,n-1 \]
采用NSM模型作为学生网络进行正向推理。除了推理损失外,还考虑了学生网络的预测和教师网络的监督信号的损失: \[ \mathcal{L}_1=D_{KL}(p_s^{(n)},p_f^*)\\ \mathcal{L}_2=\sum_{k=1}^{n-1}D_{KL}(p_s^{(k)},p_t^{(k)})\\ \mathcal{L}_s=\mathcal{L}_1+\lambda\mathcal{L}_2 \] 其中\(p_t^{(k)}\)与\(p_s^{(k)}\)是分别表示教师网络和学生网络在第\(k\)步的中间实体分布,\(\lambda\)是需要调优的参数。