- 论文:https://arxiv.org/pdf/1904.01246.pdf
Abstract
- 之前跳数固定为2或者3。UHop(unrestricted-hop framework)代替了基于关系链的搜索框架(relation-chain-based),放松了对于跳数的限制。
1. Introduction
- 之前(relation-chain-based):KBQA is decomposed into topic entity linking, which determines the starting entity corresponding to the question, and relation extraction, which finds the path to the answer node(s).In previous work, models consider all relation paths starting from the topic entity.
- Uhop: We decompose the task of relation extraction in the knowledge graph into two subtasks: knowing where to go, and knowing when to stop (or to halt). That is, single-hop relation extraction and termination decision.
2. UHop Relation Extraction
使用的数据集是already annotated with relations and paths。[原文:As some datasets are already annotated with relations and paths, direct learning using an intermediate reward is more reasonable.]
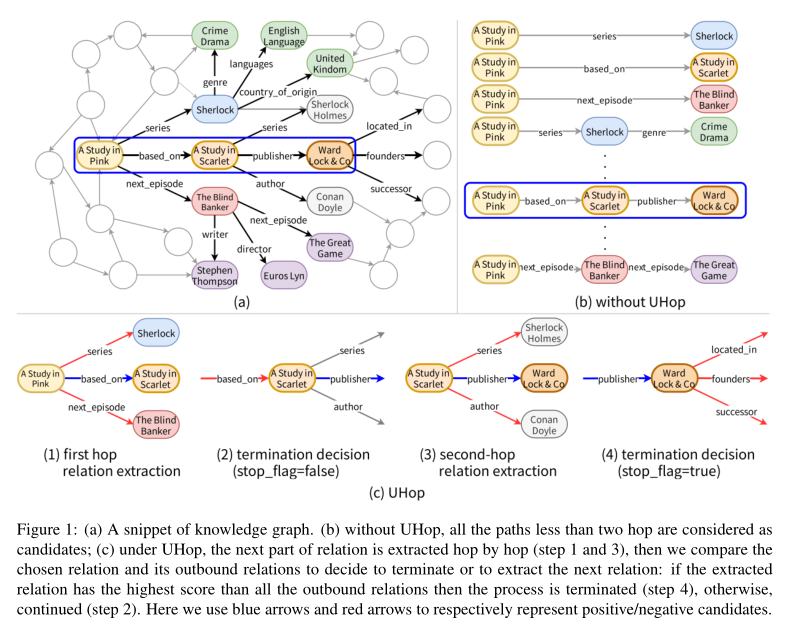
两大主要子任务:单跳关系提取(single-hop relation extraction)和比较终止决定(comparative termination decision),两个任务进行过程如下图:

需要注意的是,从第二次迭代开始,候选关系与先前选择的关系concatenate在一起,以记住历史并将其作为一个整体来考虑。
继续的话:the model prefers the correct \(\hat r\) over the other relations \(R−\hat r\) of \(e\)
停止的话:the model favors the correct relation \(\hat r\) linked to the current entity \(e\) over the outbound \(R\) relations from \(e\).
与之前方法的区别如下:
3.1 单跳关系提取(Single Hop Relation Extraction)
给定问题\(Q\),候选关系集\(R\),一种成对分类模型(pairwise classification model)\(F\),单跳关系提取表示为: \[ r=\mathop{\arg\max}_{r\in R}\ F(Q,r) \]
Hinge loss定义为: \[ \mathcal{L}_{RE}=\frac {\sum\limits_{r \in R-\hat r}max(0,-(s^{\hat r}-s^r)+M)}{|R-\hat r|} \] \(s^{\hat r}\)和\(s^r\)分别是真实关系和候选关系的得分。
边际M(margin)是范围(0, 1]中的任意值,损失函数的目标是最大化正确预测和错误预测之间的M
3.2 比较终止决定(Comparative Termination Decision)
与单跳关系提取使用的模型相同。当模型不能提取出比前一跳更好的关系时,模型停止。
不同的是与之前已经提取出的关系\(\hat r\)比较的候选关系集合\(R\)是之前提取到的所有关系和从新的当前实体\(e\)出发的关系的concatenation。在进入终止决策前已经更新了\(e \leftarrow e'\),故如果分数\(s^{\hat r}\)高于所有比较的关系,则搜索停止;否则搜索继续。
给定问题\(Q\),从之前实体提取出的关系\(\hat r\),从新的当前实体\(e\)出发的候选关系集\(R\),和与单跳关系提取相同的模型\(F\),程序可制定为: \[ f(x)= \begin{cases} True,& F(Q, \hat r)>F(Q,r)\ \forall x\in R\\ False,& F(Q, \hat r)<F(Q,r)\ \exist x\in R \end{cases} \]
损失(Loss)取决于标志stop。如果程序应该继续,即stop为false,loss被定义为: \[ \mathcal{L}_{TD}=max(0,-(s^{r'}-s^{\hat r})+margin) \] 其中\(s^{r'}\)是下一跳中与gold relation\(r'\)配对的问题的分数;\(s^{\hat t}\)是与已提取的关系\(\hat r\)配对的问题的分数。
如果该过程应该终止,则: \[ \mathcal{L}_{TD}=\frac {\sum\limits_{r \in R}max(0,-(s^{\hat r}-s^r)+M)}{|R|} \] 模型会学习使\(s^{\hat r}\)大于\(s^r\),从而导致关系提取终止。
3.3 动态问题表示(Dynamic Question Representation)
定义一个动态问题表示生成函数\(G\)来更新每一跳的问题表示。给定先前选择的关系路径\(P\)和原始问题\(Q\),\(G\)通过\(Q'=G(Q,P)\)来生成新的问题表示。假设当提取下一个关系时,由于当前关系已被选择,则它在问题中的相关信息就失去了重要性。
考虑到模型体系中注意力层的存在,提出了两种更新问题表示的方法。
- 对于注意力模型,我们通过以下方式直接利用注意力权重作为动态问题表示生成函数的一部分:
\[ G(Q,P)=W(Q-attention(Q,P))+B \]
- 对于无注意力模型,我们使用线性变换函数作为\(G\)应用于先前选择的关系和问题表示的concatenation上,以产生新的表示: \[ G(Q,P)=W[Q:P]+B \] 其中\(W\)和\(B\)都是训练要优化的权重矩阵。
3.4 联合训练子任务(Jointly Trained Subtasks)
- 在训练中,我们联合优化了UHop的两个子任务。对于每个问题及其候选,损失函数定义为: \[ \mathcal{L}=\sum_i^H(L_{RE}^{(i)}+L_{TD}^{(i)}) \] 其中,\(H\)是在gold 关系路径中的跳数;\(\mathcal{L}_{RE}^{(i)}\)和\(\mathcal{L}_{TD}^{(i)}\)是两个子任务在第\(i\)跳的损失函数。