贝叶斯模型

1. 最大似然估计(MLE)

概率是已知模型和参数，推数据。统计是已知数据，推模型和参数

最大似然估计是求参数θ，使似然函数P(x|θ)最大。

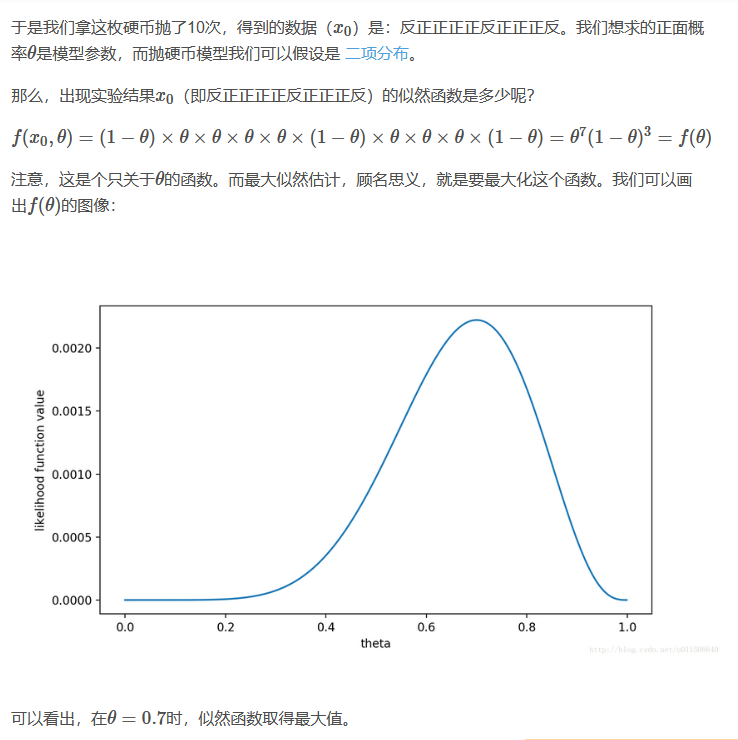
例：抛硬币，设正反面出现的概率记为θ，如图

2. 最大后验概率估计(MAP)

最大似然估计是求参数θ, 使似然函数P(x|θ)最大。

最大后验概率 (MAP) 估计则是求参数θ，使后验概率P(θ|x)最大。即使得P(x|θ)P(θ)最大(贝叶斯公式)。(x一般是一个确定的值，故一般P(x)也是一个确定值而省略)

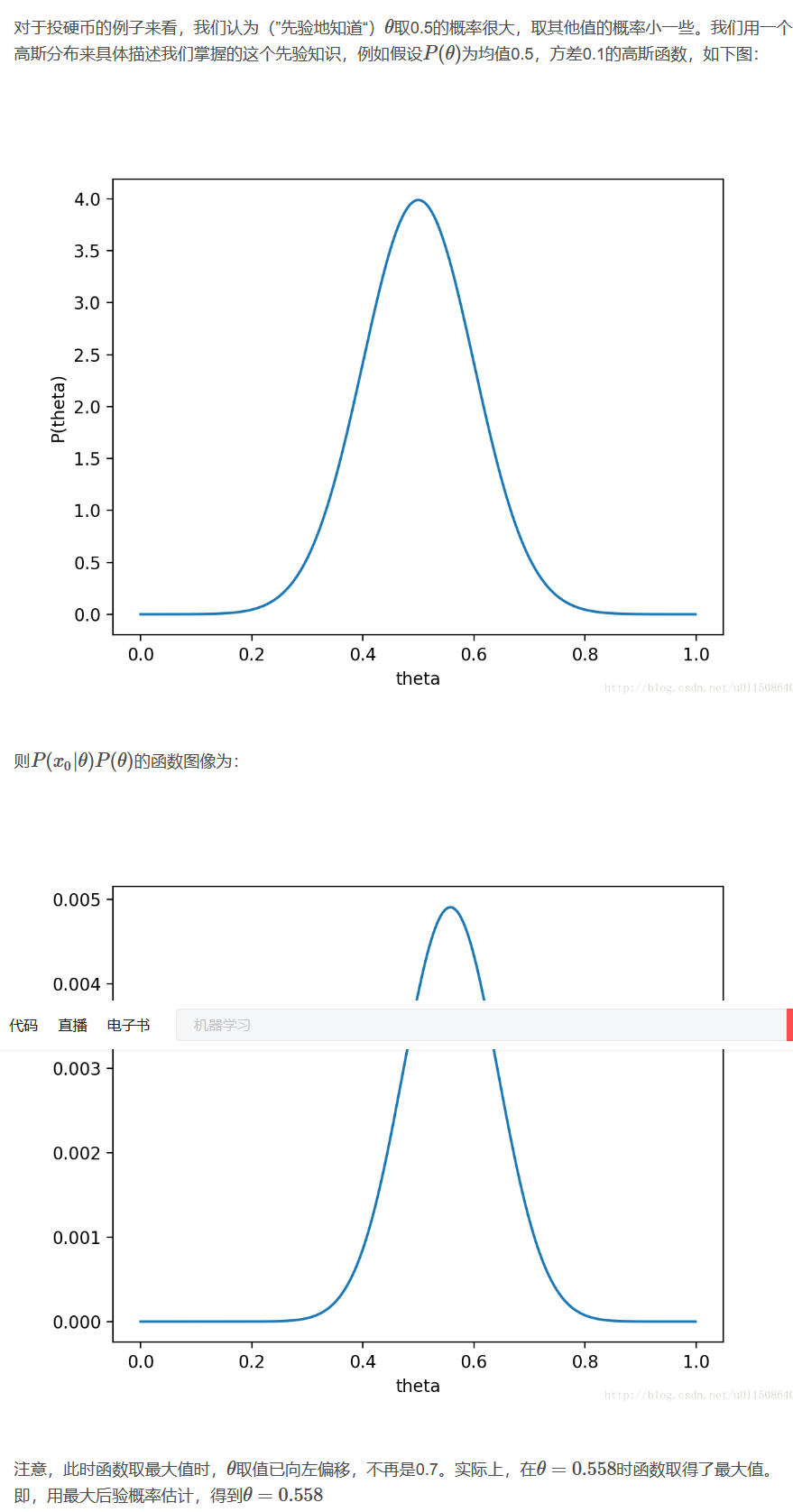
例：抛硬币

3. 贝叶斯分类

3.1 基本术语

P(A)是A的先验概率或边缘概率
P(A|B)是条件概率，A的后验概率
P(B|A)是条件概率，B的后验概率
P(B)是B的先验概率或边缘概率，也作标准化常量

Bayes定理可表述为：A的后验概率=(类似度*先验概率)/标准化常量，也就是说，后验概率与先验概率和类似度的乘积成正比。另外，比例P(B|A)/P(B)也有时被称作标准类似度（standardised likelihood），Bayes定理可表述为：后验概率 = 标准类似度*先验概率。

3.2 贝叶斯公式推导

3.3 贝叶斯的应用

3.3.1 贝叶斯的应用

拼写纠正

P(我们推測他想输入的单词 (h#)| 他实际输入的单词(D))

即对于不同的推测h1、h2、h3，计算：

P(h#|D) = P(h#) * P(D|h#) / P(D)

对于不同h#，P(D)都是一样的，故比较时可省略，即

P(h# | D) ∝ P(h#) * P(D | h#) 。

例：想打the，打成了thew。用户实际是想输入 the 的可能性大小取决于 the 本身在词汇表中被使用的可能性（频繁程度）大小（先验概率）和想打 the 却打成 thew 的可能性大小（似然）的乘积。
中文分词

令X为字串(句子)，Y为词串(分词结果)

即寻找最大的**P(Y|X) ∝ P(Y)*P(X|Y)，可表述为：这样的分词方式（词串）的可能性乘这个词串生成句子的可能性**。

一般分词是肯定能组成句子的，所以近似将P(X|Y)看作是恒等于1的。故问题转化为最大化P(Y)，即寻找一种分词使得这个词串（句子）的概率最大化。

计算方法：对于词串中不同分词W#，依据联合概率的公式展开：P(W1, W2, W3, W4 ..) = P(W1) * P(W2|W1) * P(W3|W2, W1) * P(W4|W1,W2,W3) * ..，通过计算一系列条件概率来计算。

存在问题：随着条件数目的增加（例最后一项的条件数目有n-1项），数据稀疏问题会越来越严重（维度灾难），即便语料库再大也无法统计出一个靠谱的P来。故根据马尔科夫假设（Markov Assumption）：句子中一个词的出现概率仅仅依赖于它前面的n个词（一般n不超过3），提出了N-gram模型（以下开小差讲解N-gram）。
- N-gram的用途：
  - 词性标注（将词性标注看成一个多分类问题，计算每个词性的概率）
  - 垃圾短信分类（给短信的每个句子断句，用N-gram判断每个句子是否是垃圾短信中的敏感句子，若敏感句子个数超过一定阀值，认定整个邮件是垃圾短信）
  - 分词器
- N-gram中N的确定
  
  使用Perplexity指标，该指标越小表示一个语言模型的效果越好。针对不同的N-gram，计算各自的Perplexity。
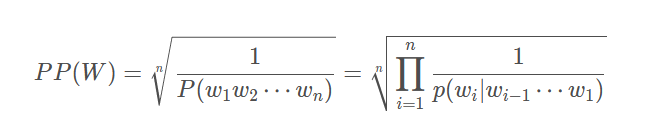
- N-gram中的数据平滑方法
  
  当N变大时，会出现稀疏问题。故需要进行数据平滑。数据平滑的目的有两个：一个是使所有的N-gram概率之和为1，并且使所有的n-gram概率都不为0。本质是重新分配整个概率空间，使已经出现过的n-gram的概率降低，补充给未曾出现过的n-gram。
  - 拉普拉斯平滑
  - 内插与回溯
与朴素贝叶斯算法思想上一致。有了这个假设，复杂的乘积可改写为： P(W1) * P(W2|W1) * P(W3|W2) * P(W4|W3) .. （n=1时）。

例：一个字串X为：“南京市长江大桥”。对于不同分词结果：“南京市长/江大桥”或者“南京市/长江大桥”，由于“南京市长”和“江大桥”在语料库中一起出现的频率为 0 ，这个整句的概率便会被判定为 0 。从而使得“南京市/长江大桥”这一分词方式胜出。

3.3.2 朴素贝叶斯模型(Naive Bayesian Model, NBC)

比较广泛使用的两种分类模型时决策树模型(Decision Tree Model)和朴素贝叶斯模型(Naive Bayesian Model, NBC)

当影响事情的因素有多个时，公式可写做：

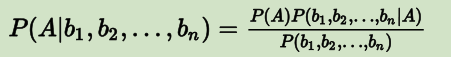
式中P(A)和多个因素的联合概率P都是可以单独计算的，与A和bi之间的关系无关，故此两项可看作常数。对于求解P(A|b1, b2,..., bn)，最关键的是P(b1, b2,..., bn)。根据链式法则可得：

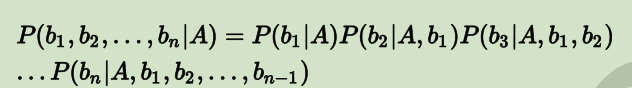
若b1到b2这些特征之间是条件独立的，则P(bi | A, bj)=P(bi | A)，就有

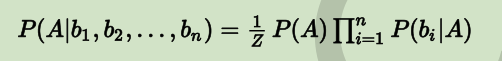
(Z对应P(b1, b2,..., bn))

上式中的b1到bn是特征，A是最终的类别，所以可惜而为如下公式：

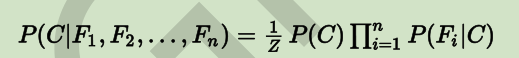
这个公式也就是我们的朴素贝叶斯分类器的模型函数。其中因为公式Z对应的P(b1, b2,..., bn)永远都是固定不变的，因此可直接省去分母部分

用法如下：

有一个朴素贝叶斯分类器，能够区分出k个类（c1, c2,..., ck），用来分类的特征有n个：（F1, F2,..., Fn）
现有个样本s，我们要用NB分类器对它进行预测，则需要先提取出这个样本的所有特征值F1到Fn，将其代入下式（因为对应不同分类的分母为固定值，所以公式可简化为如下形式）中进行k次运算：
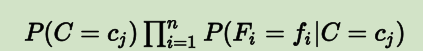
然后比较这k次的结果，选出使得运算结果最大的那个cj（j=1, 2,..., k）——这个cj对应的类别就是预测值。求上式的最大值也可以用如下公式表示：
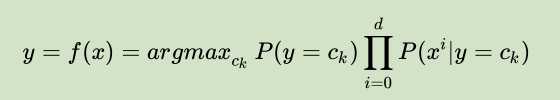
设我们当前有一个模型，总共只有两个类别：c1 和 c2；有三个 Feature：F1，F2和F3。F1 有两种可能性取值：f11 和 f12；F2 有三种可能性取值：f21，f22，f23；F3 也有两种可能性取值：f31，f32。

则对于此模型，我们要做的是通过训练过程，获得下面这些值：

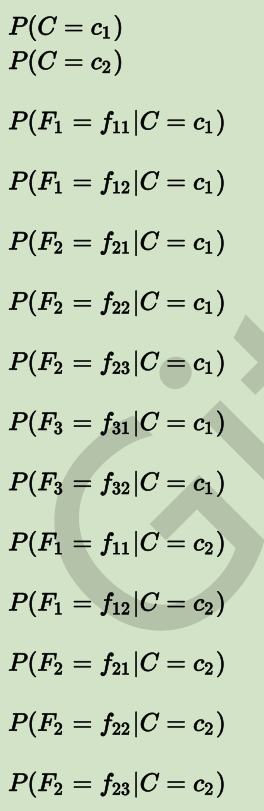
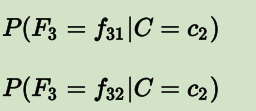
之后即可进行预测：

注：符号“∝”表示成正比例，值得注意的是P(C=c1|x)与P(C=c2|x)这两个值之和不为1是因为这里的计算并没有带入分母，这也是主里引入正比符号的原因，但是不引入分母对于实际分类的对比是没有影响的。