NLP
[[MLE+MAP+贝叶斯+n-gram#3 3 1 贝叶斯的应用|N-garm]]
贝叶斯公式: \[ P(A | B)= \frac {P(B|A)P(A)}{P(B)} \]
马科夫假设:句子中一个词的出现概率仅仅依赖于它前面的若干个词。此假设即可在一定程度上解决维度灾难(curse of dimensionality)问题。由此引入Bi-gram与Tri-gram。
Bi-gram:只依赖它前面出现的一个词 \[ p(S)=p(w_1w_2w_3...w_n)=p(w_1)p(w_2|w_1)...p(w_n|w_{n-1}) \] Tri-gram:只依赖于它前面出现的两个词 \[ p(S)=p(w_1w_2...w_3)=p(w_1)p(w_2|w_1)...p(w_n|w_{n-1}w_{n-2}) \]
数据平滑(data Smoothing):理论上N越大效果越好,但是N过大会出现稀疏问题(Sparsity)。故需进行数据平滑,目的有两个:使所有N-gram概率之和为1,使所有的N-gram概率都不为0。本质其实就是重新分配整个概率空间,使已经出现过的n-gram的概率降低,补充给未曾出现过的n-gram。常见平滑方法有插值平滑(Interpolation)与回溯法(backoff),具体核心思想不再赘述。
存在问题:不考虑超过1个或者2个单词的上下文(n),无法计算词汇间的相似度。
NNLM
创新:提出词向量、引入神经网络。
模型结构:
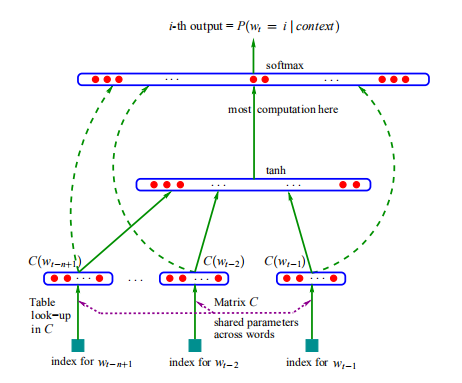
输入层:
one-hot vector形式的编码,对于每个one-hot vector\((1 × |V|)\),与Embedding size为\(m\)的矩阵\(C (|V| × m)\)相乘,得到一个distribution vector\((1 × m)\)(此处即选择C中相应对应词向量的那一行)。\(m\)比|V|小很多,从而达到了降维的目的,同时 \(C\) 可由神经网络的Back propagation训练不断优化。
隐藏层:
得到所有词的词向量后(即一个 \(( n - 1) × m\) 的矩阵),进行处理得到一个 \((n - 1)m×1\)的向量\(x\)。
隐含层为一个简单的tanh激活层,公式为 \[ hidden=tanh(Hx+d) \] 其维度信息为: \[ H:h×(n-1)m\\ d:h×1\\ x:(n-1)m×1 \]
输出层
利用了隐藏层的输出及原始词向量,最后还需用\(softmax\),具体公式如下: \[ y=b+Wx+Utanh(Hx+d) \] 其维度信息为: \[ U:|V|×h\\ W:|V|×(n-1)m\\ b:|V|×1 \] 若不想利用原始词向量信息则将\(W\)设置为零矩阵
损失函数为 \[ L=\frac {1}{T}\sum_{t}log\tilde{P}(w_t|w_{t-1},...w_{t-1+n})+R(\theta) \] \(R(\theta)\)为正则化项 \[ \theta=(b,d,W,U,H,C)\\ \theta\leftarrow\theta+\epsilon\frac{\partial{log\tilde{P}(w_t|w_{t-1},...,w_{t-n+1})}}{\partial\theta} \]
存在问题
NNML只用了左边的n-1个词,不能利用更多的上下文信息(如2010年Mikolov提出RNNLM)
NNML的输出层计算量太大,需减少计算量使得大规模语料上的训练变得可行(如Minh和Hinton提出的LBL以及后续的一系列模型)
优化(简要):
2007年Mnih和Hinton提出的LBL以及后续的一系列相关模型,省去了NNLM中的激活函数,直接把模型变成了一个线性变换,尤其是后来将Hierarchical Softmax引入到LBL后,训练效率进一步增强,但是表达能力不如NNLM这种神经网络的结构;
2008年Collobert和Weston提出的C&W模型不再利用语言模型的结构,而是将目标文本片段整体当做输入,然后预测这个片段是真实文本的概率,所以它的工作主要是改变了目标输出,由于输出只是一个概率大小,不再是词典大小,因此训练效率大大提升,但由于使用了这种比较“别致”的目标输出,使得它的词向量表征能力有限;
2010年Mikolov提出的RNNLM主要是为了解决长程依赖关系,时间复杂度问题依然存在。
Word2vec
两种模型and两种优化算法
- \(CBOW\)(连续词袋模型):利用上下文预测中心词
- \(Skip-gram\)(跳字模型):利用中心词预测上下文
- \(hierarchical\ softmax\)(层次\(softmax\))
- \(negative\ sampling\)(负采样)
与NNLM的区别
不涉及两个优化算法的角度讲,word2vec本质上是描述从自然语言到词向量转换的技术,同时蕴含语义信息:语义相近的词映射到欧式空间后具有较高的余弦相似度。NNML是把上下文词的向量进行拼接,word2vec是进行sum,求平均值来转换成低维词向量。
涉及的两个优化算法可在一定程度上解决NNLM模型中出现的从隐藏层到输出到\(softmax\)层的计算量很大的问题,因为NNLM要计算所有词的\(softmax\)概率,再去寻找最大值。而word2vec采用了哈夫曼树来代替从隐藏层到输出\(softmax\)层的映射从而避免计算所有词的\(softmax\)概率。在实际计算中,只需沿着哈夫曼树从根结点走到叶节点即可。时间复杂度从\(O(n)\)降低到\(O(logN)\)
利用$ CBOW $模型理解流程
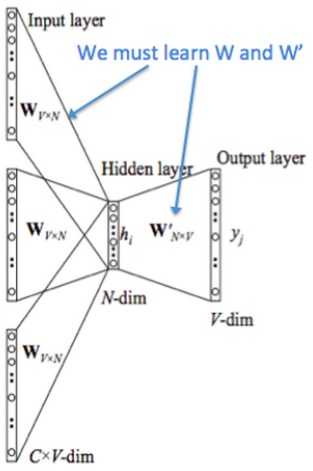
- 输入层:上下文单词的one-hot【假设单词向量空间dim为V,上下文单词个数为C,组合起来维度信息即为:C×V,图中输入层的三个分别为三个单词的one-hot表示】
- 输入的one-hot矩阵乘以共享的输入权重矩阵W【V × N矩阵,N为自己设定的数,初始化权重矩阵W】
- **隐藏层:所得到的向量相加求平均作为隐藏层向量,size为1*N**
- 乘以输出权重矩阵\(W'\)【N×V】
- 输出层:经过\(softmax\)可得到向量【1×V】激活函数处理得到的V-dim概率分布,概率最大的即为预测出的中心词(target word)
- 代价函数:交叉熵代价函数
- 任何单词的one-hot乘以这个矩阵都将得到自己的词向量(Word Embedding)
两个优化算法的具体过程
详见:http://flyrie.top/2018/10/31/Word2vec_Hierarchical_Softmax/
https://blog.csdn.net/itplus/article/details/37998797
RNN
循环神经网络相较于普通神经网络,可结合上下文去训练模型。
Forward Propagation【此部分来自吴恩达深度学习网课】
循环神经网络隐藏层常用的激活函数是\(tanh\),输出层的激活函数采用为\(sigmoid\)函数(根据实际需要)
公式推导详解
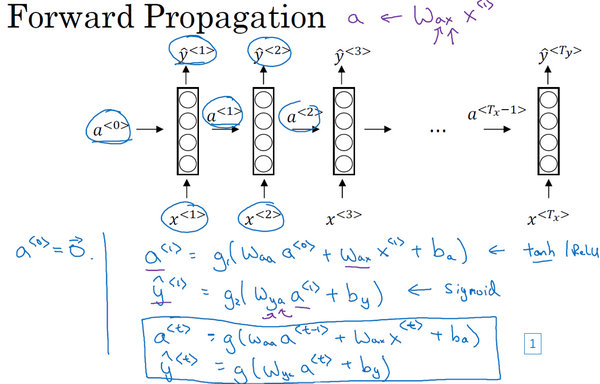
在\(t\)时刻
\[ a^{<t>}=g_1(W_{aa}a^{<t-1>}+W_{ax}x^{<t>}+b_a)\\ \hat y=g_2(W_{ya}a^{<t>}+b_y) \]
上标表示时间步,第一个字符表示将要求解的变量,第二个字符表示使用的变量
公式简化
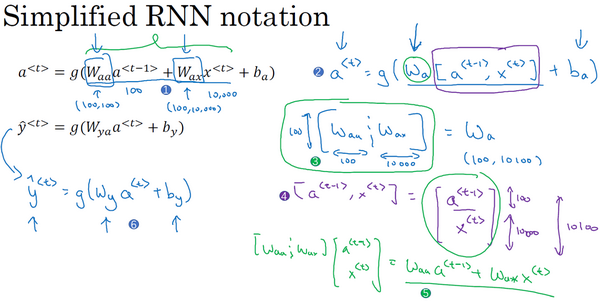
说明:为了简化将\(W_{aa}\)与\(W_{ax}\)水平放置组成\(W_a\);将\(a^{<t-1>}\)与\(x^{<t>}\)叠在一起;
更形象的总体说明:
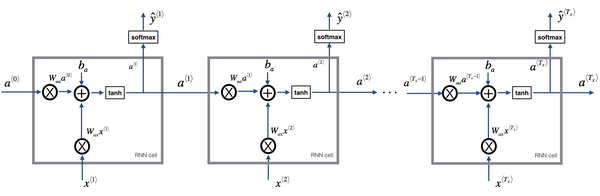
Backpropagation through time
交叉熵损失函数: \[ L^{<t>}(\hat y^{<t>},y^{<t>})=-y^{<t>}log\hat y^{<t>}-(1-y^{<t>})log(1-\hat y^{<t>}) \] 整个序列的损失函数\(L\) \[ L(\hat y, y)=\sum_{t=1}^{T_x}L^{<t>}(\hat y^{<t>},y^{<t>}) \]
更具体公式
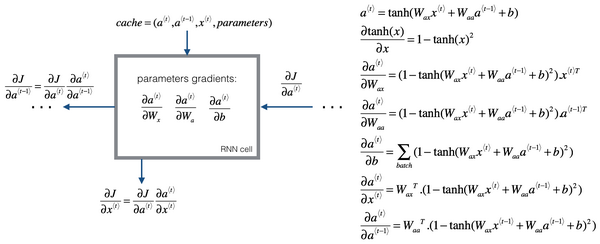
分类
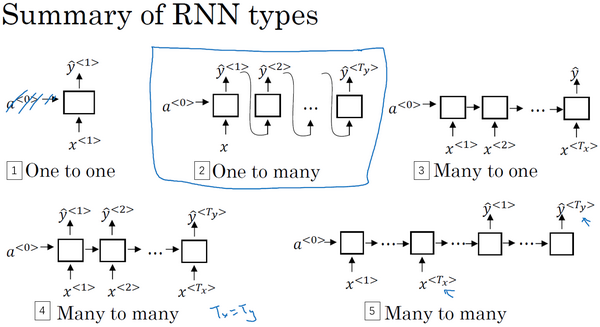
存在问题
- 梯度消失问题(Vanishing gradients with RNNs):对于很深的神经网络后面层的输出误差很难影响到前面层的计算,梯度被近距离梯度主导,导致模型很难学习到远距离的依关系,故RNN不擅长处理长期依赖问题
- 梯度爆炸问题:一般可通过梯度修剪处理
GRU
Gated Recurrent Unit(门控循环单元)
增加新变量\(c\),即代表记忆细胞\((cell)\)
\(c^{<t>}=a^{<t>}\)(与LSTMs的区别)
\(c\)的更新过程
\(\tilde c^{<t>} = tanh(W_c[\Gamma_r*c^{<t-1>},x^{<t>}]+b_c)\)
\(\Gamma_u=\sigma(W_u[c^{<t-1>},x^{<t>}]+b_u)\)【\(sigmoid\)函数,大部分情况下非常接近0或1】
\(\Gamma_r=\sigma(W_r[c^{<t-1>},x^{<t>}]+b_r)\)
\(c^{<t>}=\Gamma_u*\tilde c^{<t>}+(1-\Gamma_u)*c^{<t-1>}\)【为0则不更新】
\(u\):update
\(r\):relevance
*:每个元素相乘,而非矩阵乘法
相关门\(\Gamma_r\)门表示计算出的下一个\(c^{<t>}\)的候选值\(\tilde c^{<t>}\)与\(c^{<t-1>}\)的相关性
更新门\(\Gamma_u\)门表示更新,并且十分容易取0值,这个更新式子就会变为\(c^{<t>}=c^{<t-1>}\),有利于维持细胞的值,从而缓解梯度消失的问题,允许神经网络运行在非常庞大的依赖词上。
LSTM
long short term memory unit(长短期记忆)
\(c\)的更新过程
\(\tilde c^{<t>}=tanh(W_c[a^{<t-1>},x^{<t>}]+b_c)\)
\(\Gamma_u=\sigma(W_u[a^{<t-1>},x^{<t>}]+ b_u)\)
\(\Gamma_f=\sigma(W_f[a^{<t-1>},x^{<t>}]+ b_f)\)
\(\Gamma_o=\sigma(W_o[a^{<t-1>},x^{<t>}]+ b_o)\)
\(c^{<t>}=\Gamma_u*\tilde c^{<t>}+\Gamma_f*c^{<t-1>}\)
\(a^{<t>}=\Gamma_o*tanh(c^{<t>})\)
\(\Gamma u\):更新门
\(\Gamma_f\):遗忘门
\(\Gamma_o\):输出门
图片表述
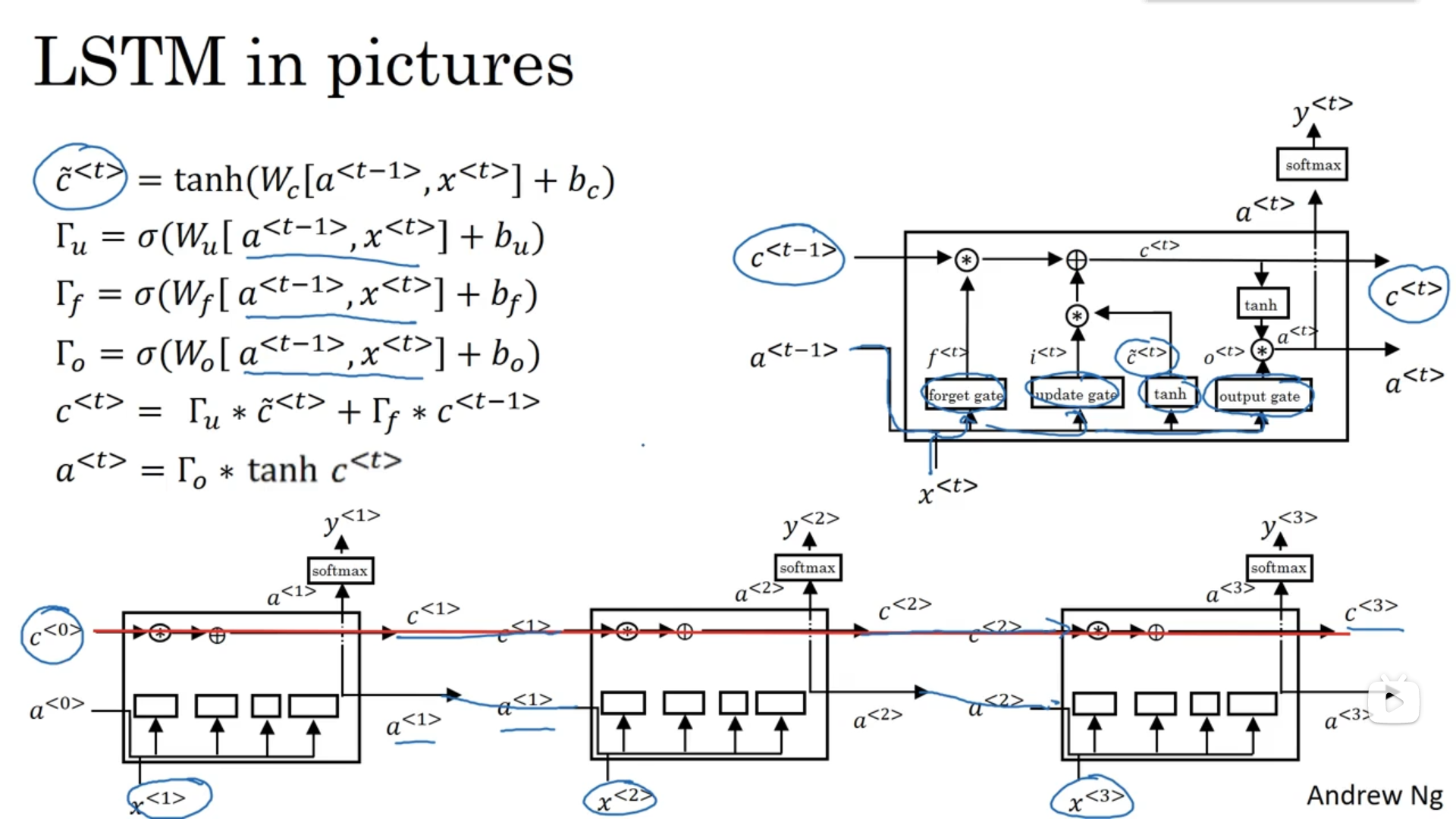
看公式可得,各门值只取决于\(a^{<t-1>}\)与\(x^{<t>}\),但有时也可以偷窥一下\(c^{<t-1>}\)的值,这叫做“窥视孔连接”\((peephole\ connection)\)。故有时说\(c^{<t-1>}\)也能影响门值。
前向传递
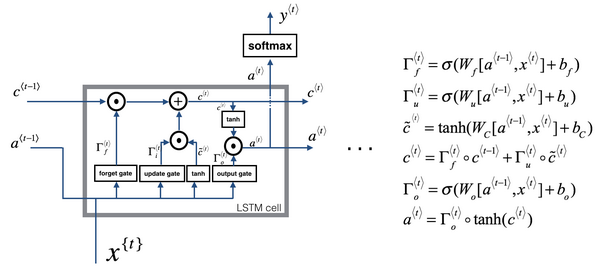
反向传播

具体推导过程见:https://zybuluo.com/hanbingtao/note/581764
Bi-directional RNN
双向循环神经网络,单元可使用标准的RNN或者GRU、LSTM单元都可,一个有LSTM单元的双向RNN模型是最常用的
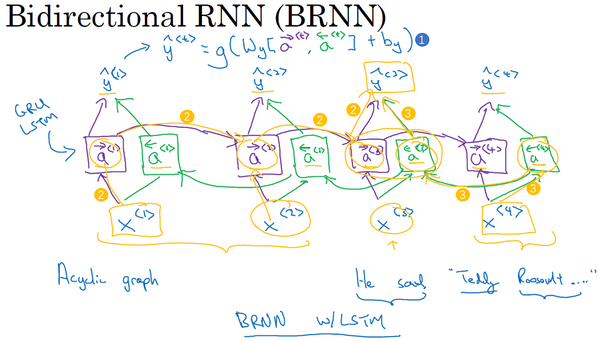
此处为标准的RNN单元\(\hat y^{<t>}=g(W_g[\vec a^{<t>}, \overleftarrow a^{<t>}]+b_y)\)
\(\overleftarrow a\)只是从右到左,也是在计算激活值
- 缺点为需要完整的数据序列
Deep RNNs
深层循环神经网络
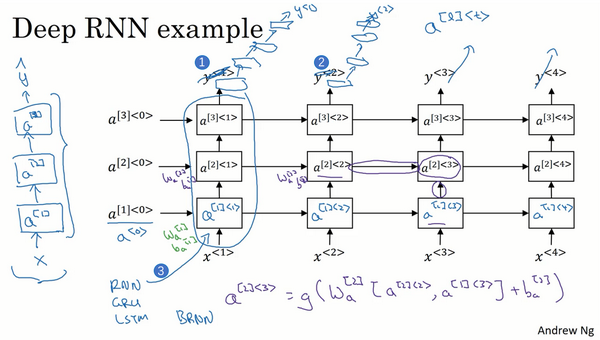
计算方法:例\(a^{[2]<3>}\)有两个输入,下面的和右面的,故可写为下式:
\(a^{[2]<3>}=g(W_a^{[2]}[a^{[2]<2>}, a^{[1]<3>}]+b_a^{[2]})\)
一般RNN不会特别深,更多会将输出去掉而换成一些深的层,这些层并不水平相连,而只是一个深层的往来,用来预测\(y\)。
TODO
- ELMo(Embeddings from Language Models)
- 为了利用无标记数据使用了语言模型
- 双向LSTM
- OpenAI GPT(Generative Pre-training Transformer)
- BERT(Bidirectional Encoder Representations from Transformers)